Marijn Heule

Marienus Johannes Hendrikus Heule (born March 12, 1979 at Rijnsburg, The Netherlands) is a Dutch computer scientist at Carnegie Mellon University who studies SAT solvers. Heule has used these solvers to resolve mathematical conjectures such as the Boolean Pythagorean triples problem, Schur's theorem number 5, and Keller's conjecture in dimension seven.

Heule received a PhD at Delft University of Technology, in the Netherlands, in 2008. He was a research scientist, later a research assistant professor, at the University of Texas at Austin from 2012 to 2019. Since 2019, he has been an associate professor in the Computer Science Department at Carnegie Mellon University.

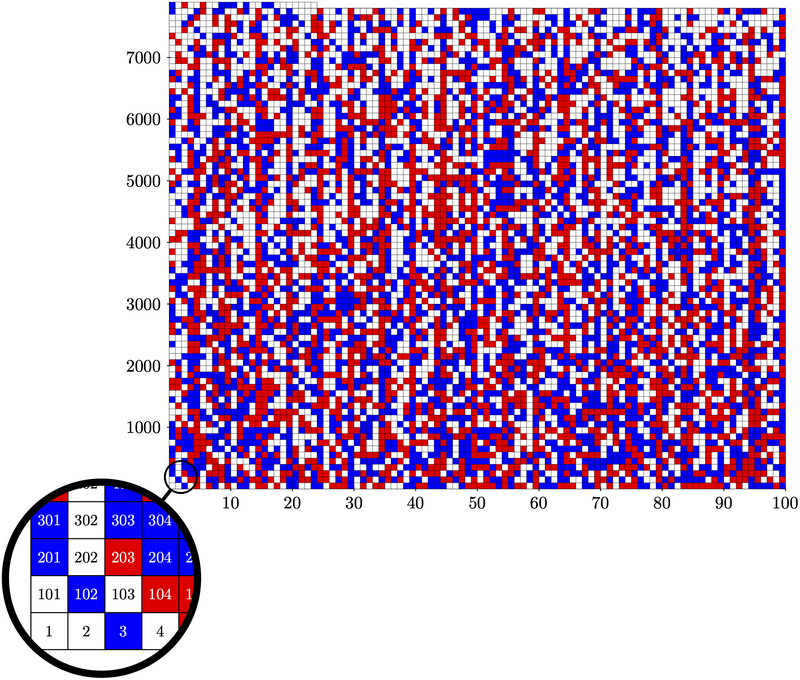
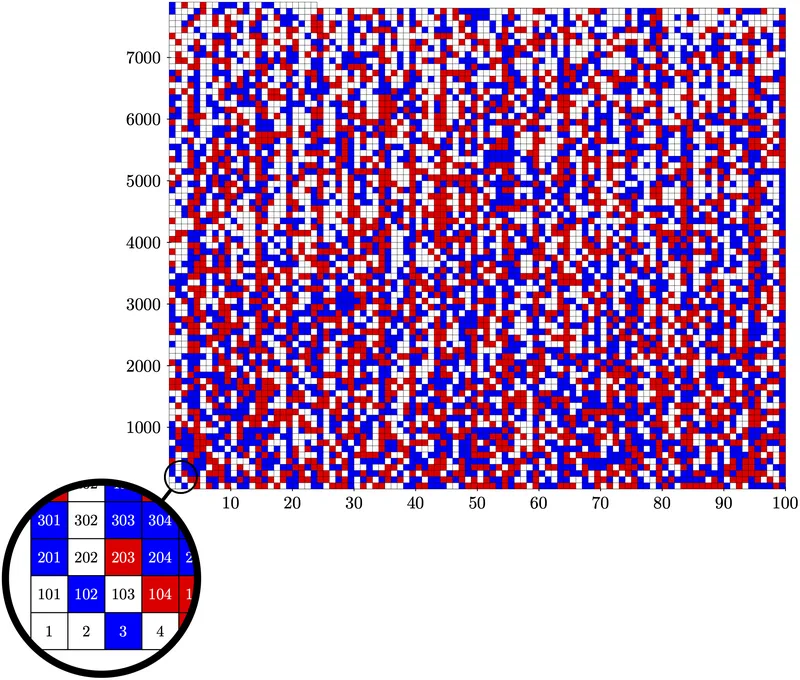
In May 2016 he, along with Oliver Kullmann and Victor W. Marek, used SAT solving to solve the Boolean Pythagorean triples problem. The statement of the theorem they proved is

To prove this theorem, the possible colorings of {1, ..., 7825} were divided into a trillion subcases using a heuristic. Each subclass was then solved a Boolean satisfiability solver. Creating the proof took about 4 CPU-years of computation over a period of two days on the Stampede supercomputer at the Texas Advanced Computing Center and generated a 200 terabyte propositional proof (which was compressed to 68 gigabytes in the form of the list of subcases used). The paper describing the proof was published in the SAT 2016 conference, where it won the best paper award. A $100 award that Ronald Graham originally offered for solving this problem in the 1980s was awarded to Heule.

He used SAT solving to prove that Schur number 5 was 160 in 2017. He proved Keller's conjecture in dimension seven in 2020.

In 2018, Heule and Scott Aaronson received funding from the National Science Foundation to apply SAT solving to the Collatz conjecture.

In 2023 together with Subercaseaux, he proved that the packing chromatic number of the infinite square grid is 15